Técnicas de planificación.

CARTA GANTT

PERT (Program Evaluation & Review Technique

CPM (Critical Path Method)

MCE (Minimum Cost Expediting)

Método de ROY

Método GERT (Graphical Evaluation & Review Technique)

Descripción técnica 

CARTAGANTT: es una popular herramienta gráfica cuyo objetivo es mostrar el tiempo de dedicación previsto para diferentes tareas o actividades a lo largo de un tiempo total determinado. A pesar de que, en principio, el diagrama de Gantt no indica las relaciones existentes entre actividades. La posición de cada tarea a lo largo del tiempo hace que se puedan identificar dichas relaciones e interdependencias. Fue Henry Laurence Gantt quien, entre 1910 y 1915, desarrolló y popularizó este tipo de diagrama en Occidente.

PERT (Program Evaluation & Review Technique): Creado para proyectos del programa de defensa del gobierno norteamericano entre 1958 y 1959. Se utiliza para controlar la ejecución de proyectos con gran

número de actividades desconocidas que implican investigación, desarrollo y pruebas .

CPM (Critical Path Method): Desarrollado para dos empresas americanas entre 1956 y 1958 por un equipo liderado inicialmente por James E. Kelley y Morgan R. Walker. Se utiliza en proyectos en los que hay poca incertidumbre en las estimaciones. Es prácticamente el mismo que el PERT sólo que supone conocidos los tiempos de duracin de las actividades (tiene un carácter determinista).

MCE “Minimum Cost Expediting”, “aceleración del proyecto a coste mínimo"  o PERT Coste: Es una de las variantes del CPM, pero introduciendo la relación que existe entre coste y duración de una actividad. De esta forma se obtiene la programación de proyectos a coste mínimo.

Método de ROY: Desarrollado en Europa entre 1958 y 1961 por un grupo de ingenieros encabezados por B.Roy y M. Simmonard. Similar a los métodos PERT y CPM, pero permite establecer las redes sin utilizar

actividades ficticias e iniciar los cálculos sin la construcción de la red.

Método GERT (Graphical Evaluation & Review Technique): Desarrollado por A. A. Pritsker tomando como base los trabajos de Eisner y Elmaghraby. El método GERT extiende la incertidumbre en la duración de las actividades a la propia programación, permitiendo considerar un número mayor de situaciones del proyecto que otros métodos. Las actividades precedentes de cada nudo pueden ser de naturaleza determinante o probabilística.

Uso de cada técnica

Indice:

 - CARTAGANTT

 - PERT

 - CPM

 - Método de ROY

Carta Gantt

Representación gráfica de las actividades sobre una escala de tiempos.

Las actividades se representan en forma de barra sobre dicha escala manteniendo la relación de proporcionalidad entre sus duraciones y su representación gráfica, y su posición respecto del punto origen del proyecto.

– No permiten la representación de conexiones cruzadas que muestre directamente la dependencia de tareas.

– Tampoco permiten conocer claramente la lógica utilizada en la planificación.

Los grafos son la base de la mayoría de los métodos de planificación temporal.

Un grafo se puede definir por medio de dos conjuntos:

– Un conjunto X que representa n puntos del plano denominados vértices.

– Un conjunto U que representa las relaciones que existen entre los elementos del conjunto X . Dichas relaciones se denominan arcos.

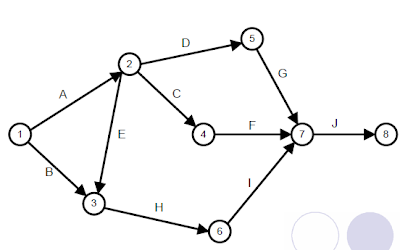
PERT

El método PERT parte de la descomposición del proyecto en actividades. Se establece también el concepto de suceso: acontecimiento que indica el principio o fin de una actividad o conjunto de actividades. No consume tiempo ni recursos. El método utiliza una estructura de grafo para la representación gráfica de las actividades o tareas de un proyecto, sus tiempos de comienzo y finalización y las dependencias entre las distintas actividades.

Construcción del grafo PERT

Prelaciones: Se comienza recogiendo de manera sistematizada toda la información referente a las prelaciones entre las distintas actividades. Existen dos procedimientos:

– Matriz de encadenamientos: matriz cuadrada cuya dimensión es igual al número de actividades en que se ha descompuesto el proyecto. Si en los puntos de cruce aparece una X indica que para poder iniciar la actividad de la fila tiene que haber terminado la correspondiente a la columna.

– Cuadro de prelaciones: tabla de dos columnas, en la primera se encuentran las actividades del proyecto y en la segunda figuran las actividades precedentes de su homologa en la primera columna.

  

Construir el grafo: El grafo comienza en un vértice que representa el suceso inicio del proyecto y termina en otro vértice que representa el suceso fin del proyecto.

– Suceso inicio del proyecto: representa el inicio de una o más actividades pero no representa el fin de ninguna.

– Suceso fin del proyecto: representa el fin de una o más actividades pero no representa el comienzo de ninguna.

– Actividades inicio del proyecto: no tienen ninguna actividad precedente.

– Actividades fin del proyecto: no preceden a ninguna otra actividad.

La numeración de los vértices del grafo debe cumplir siempre la siguiente condición:

El número del vértice que represente el comienzo de cierta actividad debe ser menor que el número del vértice que represente el suceso fin de esa actividad.

Asignación de tiempos a las actividades

La duración de una actividad no puede fijarse, en la mayoría de los casos, con exactitud. Depende de circunstancias aleatorias (averías en las máquinas, cortes de energía eléctrica, retraso en la entrega de suministros, enfermedad del personal,. . .). Este problema es abordado por el método PERT de modo muy peculiar, pues considera tres estimaciones de tiempo distintas:

– Estimación optimista (Eo): tiempo mínimo en que podría ejecutarse la actividad i si no surgiera ningún contratiempo.

– Estimación más probable o estimación modal (Em): tiempo que se empleará en ejecutar la actividad i en circunstancias normales.

– Estimación pesimista (Ep): tiempo máximo de ejecución de la actividad i si las circunstancias son muy desfavorables.

Cálculo de los tiempos EET y LET Una vez construido el grafo del proyecto y asignados tiempos de ejecución a las actividades, el siguiente paso consistirá en calcular dos parámetros para cada suceso:

Sea tij el tiempo PERT de una actividad (i,j):

EET (Earliest Even Time): Se define el tiempo más pronto posible (“early”) de un suceso j. Representa el tiempo mínimo hemos de emplear para poder empezar cualquier actividad que salga del suceso j. El EET del suceso inicial es cero, para el resto de los sucesos el EET se calcula siguiendo las siguientes reglas:

•       Seleccionar todas las actividades que llegan al suceso.
•       Para cada actividad que entra, se suma la duración de la actividad y el tiempo early, EET de su suceso inicial.
•    Seleccionar el EET más alto que se haya obtenido.

LET (Latest Even Time): Se define como el tiempo más tarde permisible (“last”) de un suceso i . Representa lo más tarde que puede llegar a ese suceso, sin que afecte a la duración del proyecto.

•        El suceso fin del proyecto tiene LET igual al EET, para el resto de los sucesos se aplican las reglas siguientes: Considerar todas las actividades que salen del suceso.
•       Restar al LET del suceso final la duración de cada actividad.
•      Seleccionar el menor LET que se haya obtenido.

La verdadera importancia de los tiempos “más pronto posible” y “más tarde permisible” es que constituyen la base para el cálculo de las y p holguras, que son la pieza fundamental en todo el proceso de análisis del método PERT.

La holgura de cierto suceso i (Hi) se define como la diferencia entre los tiempos LET y EET: indica el número de unidades de tiempo en que puede retrasarse la realización del mismo, de manera que la duración del proyecto no experimente ningún retraso.

Holgura total de cierta actividad ij (HT ij) se define como el tiempo que resulta de restar el tiempo LET del suceso final del EET del suceso inicial y la duración de esa actividad.

La holgura total de una actividad indica el número de unidades de tiempo en que puede retrasarse la realización de la actividad con respecto al tiempo PERT previsto, de manera que la duración del proyecto no se retrase.

Aquellas actividades cuya holgura total sea cero se denominan actividades críticas. El camino que forman se denomina camino crítico. El retraso en la realización de cualquiera de las actividades críticas producirá un retraso en la finalización del proyecto.

CPM

CPM : Método del Camino Crítico (Critical Path Method)

Fue Diseñado Casi simultáneamente con el PERT solo que fue desarrollado por la Compañía E. I. Du Pont.

Se diferencia con el PERT básicamente en que su manejo de tiempos es determinístico, por tanto se estima un único tiempo que no esta sujeto a variaciones, supone que no hay cambios en la duración establecida.

Metodología:

 El proceso es muy similar al de PERT, sus tiempos tempranos y tardíos se calculan en forma similar.

Otra forma de trabajar bajo CPM se describe a continuación. Una vez segmentado el  proyecto en actividades, hecha la valoración de las mismas y establecidas las dependencias, se procede a diseñar el proyecto siguiendo los siguientes pasos:

Se dibuja un diagrama con todas las actividades y sus relaciones. Todas las actividades que no tienen predecesoras comienzan en el nodo 1. El último nodo debe ser el número más alto. Si es necesario, se pueden utilizar actividades con duración cero, denominadas dummy.

Se construye una tabla donde se muestran cada una de las actividades del proyecto.

En las tres filas siguientes de la tabla, se definen los nodos (la palabra “Nodos” en la primera, el nodo de comienzo de cada actividad en la segunda y en la tercera, el nodo de terminación).

A continuación, en la fila siguiente, la palabra “Tiempo” y en la fila inferior, la duración de cada actividad.

Después se pondrá la palabra “Caminos” y, bajando, se definen los posibles caminos del proyecto (uno por fila), indicando con un uno cuando la actividad correspondiente intervenga en el camino y con un cero cuando no.

En las mismas filas de cada camino y a continuación de la última columna que tendrá la última actividad del proyecto, se calcula la duración del camino, correspondiente a dicha fila, sumando los resultados de multiplicar los valores de la fila (sucesión de unos y ceros) por la fila de los tiempos de las actividades.

Se determina la suma mayor, que representará la duración del proyecto, y las actividades que forman el camino crítico vendrán dadas por aquellas actividades del camino crítico que tengan un uno.

Es importante destacar que debido a la principal característica del sistema CPM (la ausencia total de varianza y por tanto ausencia de incertidumbre) este permite hacer un manejo lineal de los costos y de sus tiempos. En el CPM no se habla de estimaciones ni de aproximaciones sino de valores exactos y predecibles lo que permite llevar su manejo en forma proporcional.

Lo anterior permite hacer reducciones de tiempos en función de unos costos por inversión en recursos, y se pueden aplicar modelos de optimización (programación matemática) lo que no ocurre con los modelos bajo incertidumbre como PERT. En estos últimos de hace solo un control presupuestal constante y las inversiones se hacen mas en aseguramiento de un valor, disminuir la incertidumbre.

Ejemplos:

ROY.

• Es otro modelo matemático de planificación, fue desarrollado en Francia por el matemático Bernard Roy, se le conoce también como el método de los potenciales o MPM y, a semejanza del Pert, ofrece una serie de planes alternativos; suele complementarse con algún sistema gráfico a efectos de representación.
• Se diferencia del PERT/CPM básicamente en dos aspectos, en su construcción y en el tipo de relaciones que se pueden manejar entre actividades.
• El Roy permite relaciones Fin-Comienzo y Comienzo-Comienzo mientras PERT/CPM solo relaciones Fin-Comienzo.
• En su representación gráfica para el Roy los Nodos o vértices del grafo representan a las actividades y los arcos o flechas tan solo las relaciones entre ellas.
• El modelo consta de unas reglas de representación de actividades, con sus relaciones y duraciones, basadas en la teoría de grafos, de una metodología de representación de datos, cálculos y resultados y de unas rutinas de cálculo basadas en algoritmos matemáticos de tipo iterativo.
• Los nodos siempre están representados por cuadros o rectángulos y no por circunferencias y concepto de eventos como el PERT/CPM no esta tan específico.

Normas de Construcción:

•  Los vértices del grafo representan las actividades.
•  Los arcos del grafo indican las relaciones entre actividades, el orden en que deben ser ejecutadas.
•  No existen sucesos ficticios ni actividades ficticias (excepto las actividades de inicio y fin).
•  Para representar las actividades se utilizan rectángulos:

1: Código de Actividad

2: Tiempo mínimo de comienzo

3: Tiempo máximo de comienzo

4: Duración de la actividad

Normas de representación:

•  Para representar las relaciones de dependencia entre actividades, se utilizan los arcos del grafo, sobre los que se inscribe la duración de la actividad precedente, permitiendo incluir el concepto de demora.
•  Los diferentes casos que admite el modelo son:

Relación final/comienzo con demora D: siempre se debe colocar sobre el arco un valor equivalente a la duración más el retardo o demora D, así:

Normas de representación:

•  Relación comienzo/comienzo con demora D: siempre se debe colocar sobre el arco un valor equivalente al retardo o demora D así, siempre y cuando el retraso sea menor que la duración de la actividad predecesora:

A continuación se podrá ver como hacer el diagrama en diversas situaciones comparándolo con PERT/CPM

Metodología:

•  Una vez segmentado el proyecto en actividades, hecha la valoración de las mismas y establecidas las dependencias, se procede p a diseñar el proyecto siguiendo los siguientes pasos:
•  Se comienza por asignar una actividad “principio” con un tiempo mínimo de comienzo de 0 y una duración 0; por tanto, el tiempo mínimo de comienzo de las primeras actividades reales del proyecto es 0.
•  A continuación se van dibujando las restantes actividades con sus correspondientes dependencias hasta llegar a la última o últimas, que terminarán en una actividad ficticia de “fin”, con duración cero.
•  Cálculo de tiempos:
•  Los tiempos mínimos de comienzo de las actividades se fijan de acuerdo con el procedimiento que se indica a continuación: el tiempo mínimo (ti) de comienzo de una actividad i es el mayor de las sumas del tiempo mínimos de las actividades precedentes (ti-1) más el valor del arco correspondiente.
•  Se prosigue con el cálculo de dichas tiempos mínimos hasta llegar al suceso “fin de proyecto”, el cual nos indica el tiempo mínimo necesario para realizar el proyecto.
•  Para calcular el tiempo máximo, se parte del suceso “fin de proyecto”, en el que se pone el tiempo máximo igual al tiempo mínimo previamente calculado, siendo éste la duración del proyecto.
• Se prosigue con el cálculo de dichos tiempos máximos de comienzo de las actividades (Ti), restando del tiempo máximo de la actividad (Ti+1) el valor del arco correspondiente que nace en la actividad i; en caso de que exista más de una actividad que nazca en la actividad i, haríamos el mismo cálculo para cada una de ellas y elegiríamos el menor.

•  Cálculo de actividades:

La holguras de

•  La holgura total de cada actividad se calcula mediante la diferencia entre sus tiempos máximo y mínimo.
•  La holgura libre de una actividad cualquiera se fija obteniendo el mínimo del resultado de calcular:

HL (i) = ti+1 – (ti+V)

Donde:

HL (i)  : holgura libre de la actividad i

ti+1     : tiempo mínimo de comienzo de la actividad siguiente a i

ti          : tiempo mínimo de la actividad i

V          : valor del arco que va de la actividad i a la actividad i+1

•  El camino crítico viene indicado por aquellas actividades que tienen holgura total nula.

Cálculo de tiempos por la matriz de Encadenamiento:

• Por medio de la matriz podemos calcular los tiempos máximos y mínimos de un proyecto, sin necesidad del diseño.
• Para aplicar este procedimiento se construye una matriz cuadrada con tantas filas/columnas como actividades tenga el proyecto (incluidas las de principio y fin); los elementos de la matriz tomarán como valor numérico el del arco, solo si la actividad indicada por la fila correspondiente es precedida por la indicada por la correspondiente columna.
• A la matriz así construida, se yuxtapone una fila en la parte inferior, donde se anotarán los tiempos máximos de comienzo de cada actividad, identificado por la columna correspondiente, y una columna en la parte derecha donde se registran los tiempos mínimos correspondiente a las actividades indicados por las respectivas filas.
• Se comienza por el cálculo de los tiempos mínimos, anotando 0 en la posición correspondiente a la actividad “principio”.
• Para calcular el tiempo mínimo correspondiente a la actividad i cualquiera, se suman a los elementos que aparecen en la fila, los tiempos mínimos calculados para las actividades correspondientes a las columnas en las que se encuentran dichos elementos, tomando como tiempo mínimo el máximo de estas sumas, el cual se anotará en el elemento adecuado de la columna adicional.
• Para calcular los tiempos máximos de comienzo de las actividades, se comienza por asignar a la actividad “fin” un tiempo máximo igual a su tiempo mínimo, previamente calculado.
•  Para una actividad cualquiera i consideraríamos las filas que tienen definidos elementos en la matriz en su intersección con la columna asociada a la actividad cuyo tiempo máximo se trata de calcular; estos valores se restan de los tiempos máximos de las correspondientes actividades, previamente calculados: la menor de estas restas será el tiempo máximo de comienzo de la actividad en cuestión.

Ventajas:

•  Es un método sencillo, idóneo para proyectos complejos.
•  Proporciona varios planes de ejecución.

 Desventajas:

•  Solo admite relaciones del tipo final/comienzo y comienzo/comienzo, con demora.
•  Es conveniente utilizar un método de representación gráfica como complemento.